Psychoanalysing ChatGPT using statistics to make a decent dating app

Published January 23, 2024

Amazingly, you can get a good date matchmaking algorithm from ChatGPT if you forget all those LinkedIn posts about prompt "engineering" and instead apply some statistics to ChatGPT's output.

How good? Try the Duolicious app to see for yourself!

If you want to know why it works, keep reading, because we're taking a deep dive into the psychology and data science of the Duolicious matching algorithm.

Why The Duolicious Algorithm is Pretty Good

The Duolicious matching algorithm works by finding people similar to you. While a lot of people say, "opposites attract," sociologists have actually found that people tend to date others who are more similar to each other than not. Scientists call that "assortative mating." Surprisingly, even for traits like height, where there's typically a big difference between each partner in a relationship, there's still a correlation between both partners' heights! Here's a chart from a study of two groups of married couples in Cameroon, but assortative mating happens everywhere, even in other species:

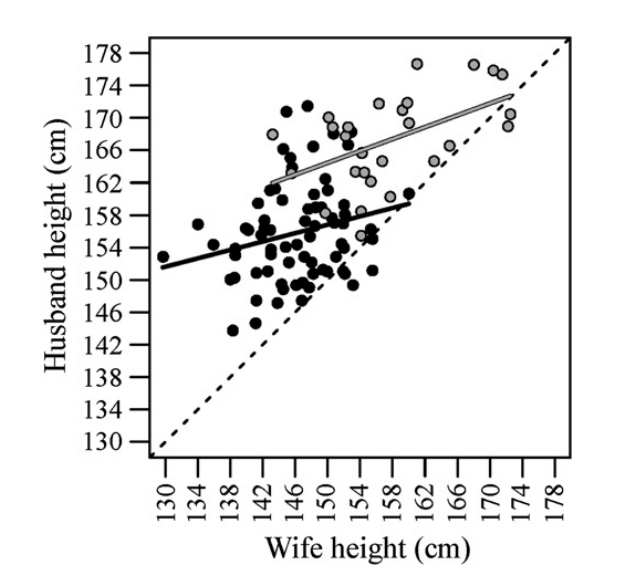
While the Duolicious algorithm doesn't take traits like height into consideration just yet, it's still pretty comprehensive. Your quick, yes-or-no answers let Duolicious measure 47 different traits related to personality, political alignment, habits, and so on. We tried to pick traits about you that stay the same over time. Personality traits like the Big 5 and MBTI definitely fit into that category. Surprisingly, political alignment tends to be fairly stable over time too; in fact it's correlated with your personality traits. Although personality traits are generally a bit more stable.

How Duolicious Figures Out What You're Like

How does Duolicious measure all those traits based on simple yes/no questions? After picking the 47 traits we want to measure, the next step is to come up with fun questions to measure them. So if we wanted to measure something like extraversion, we might invent questions like these:

Picking questions like these was the fun of making the algorithm, because it's a creative process where you basically imagine you're asking a date whatever you want. Obviously you're not totally free to ask anything, because you still need to pick questions that give you a sense of whether your imaginary date is extroverted. But it's pretty obvious to me that they do, because I've spoken with at least one human once before and I know what they're like. But computers aren't socialites like me.

So how can we get the computer to understand your answers to these questions? The obvious thing would be to ask ChatGPT—And that's pretty much what we did—But you've got to be clever about it, because there's more than 2000 questions someone can answer, which is about 40 pages! So you can't just take all of someone's answers in one blob and shove 'em in ChatGPT's face like, "here ya go!" It's just too many questions. And even if it was just one question, it'd still take too long for ChatGPT to spit out an answer for each and every person you could possibly match with.

So instead, we kind of asked ChatGPT what the questions meant once, when we made the questions. Then we distilled those answers into lists of numbers using statistics. Except it was a bit more complicated than that.

Distilling ChatGPT's Knowledge Into A Statistical Model

What we really did was ask ChatGPT to pretend to be an extrovert, then pretend to be an introvert. Then we made ChatGPT answer all 2005 questions in our question bank five times while playing those roles. Except instead of asking them as yes/no questions, we asked ChatGPT to answer on a scale from 0 to 10 (called a Likert scale, for you psychology nerds).

At this point, you might wonder, "why did you ask ChatGPT the same thing five times instead of once? And why did you make it answer on a scale from 0 to 10 if the real questions in the app are yes/no?"

You need to ask ChatGPT to answer a few times because its answers are a bit random. It's like sampling a population of real, human extroverts or introverts. Each person in the population will give you a different answer to another person. And a particular person's answers might also change depending on their mood.

As for the reason we asked ChatGPT to answer on a 0-10 scale, the short answer is that it was to get more fine-grained information without having to ask ChatGPT the same question too many times. (Even asking human users to answer the questions on a scale would give Duolicious much more info to work with. But there's a trade off between fun and accuracy, and we can easily compensate by asking users more questions.)

Anyway, once you've got ChatGPT to role-play an introvert and an extrovert a few times, you can plot its answers like this:

Does the thought of being a leader scare you?

In that plot above, we actually asked ChatGPT to answer the question 50 times for each role it played, just for demonstration purposes. You can see the shape of each distribution more clearly if you collect more answers. Here's a different question for comparison:

Does the thought of being a leader scare you?

Neat, huh?

Now brace yourself for some math. To make these pretty plots useful for making a dating matchmaking algorithm, we need to extract four things:

To make it easier to figure those out, we made a few assumptions:

None of these assumptions are accurate, but they're close enough. In the words of statistician George Box, "all models are wrong but some are useful". So with our cleverly constructed lies, we press on and do some math:

\[ \begin{align*} q_1 &= \text{cdf\_extroverts}(10) - \text{cdf\_extroverts}(5) \\ q_2 &= \text{cdf\_introverts}(10) - \text{cdf\_introverts}(5) \\ q_3 &= \text{cdf\_extroverts}(5) - \text{cdf\_extroverts}(0) \\ q_4 &= \text{cdf\_introverts}(5) - \text{cdf\_introverts}(0) \\ \end{align*} \]

Where \(\text{cdf\_introverts}\) and \(\text{cdf\_extroverts}\) are the cumulative distribution functions of our introverted and extroverted populations. We got these by using the mean and standard deviations of ChatGPT's responses to construct Gaussian distributions, then using the CDFs of those.

Then to finally get the four probabilities we were trying to extract this whole time, we do this:

\[ \begin{align*} p_1 &= q_1 / (q_1 + q_2) \\ p_2 &= q_2 / (q_1 + q_2) \\ p_3 &= q_3 / (q_3 + q_4) \\ p_4 &= q_4 / (q_3 + q_4) \\ \end{align*} \]

Using The Statistical Model To Understand You

Here's an example of the real values of those probabilities which we use in the app for the question, "Do you think it's romantic to share a last name with your partner":

\[ \begin{align*} p_1 &= 0.62 \\ p_2 &= 0.38 \\ p_3 &= 0.47 \\ p_4 &= 0.53 \\ \end{align*} \]

That means if you answer "yes" there's a 62% chance you're extroverted (and a 38% chance you're introverted). But if you answer "no", there's a 47% chance you're extroverted.

Duolicious has each of these 4 numbers stored for each of the 2005 questions and each of the 47 traits. That's \(4 \times 2005 \times 47 = 376,940\) numbers to represent our question bank, which sounds like a lot, but it's still only 0.02% of the numbers needed to store ChatGPT.

Each time you answer a question, Duolicious adds to two tallies. One keeps track of your "extroversion" score. The other keeps track of your "not extroverted" score. We get the scores just by summing the probabilities. The final number you see in the app on the "Traits" tab is:

\[ \frac{\text{ExtrovertedScore}}{\text{ExtrovertedScore} + \text{NotExtrovertedScore}} \]

Except the traits tab shows 47 traits, not 1. So there's not really 2 tallies, there's \(47 \times 2 = 94\) tallies.

How Duolicious Finds Matches Using Your Personality

To figure out your match percentage with someone else, Duolicious takes the numbers on your traits tabs and multiplies them with other peoples' numbers to compute something called the "cosine similarity" of your two personalities. It sounds complicated, but it's pretty simple, especially compared to the stats we just went through. Cosine similarity just spits out a number between 1 and -1. If we get 1, that means your personalities are totally the same and -1 means your personalities are the complete opposite. We convert that number between -1 and 1 into a percentage between 0 and 100 like this:

\[ \text{similarity\_to\_percentage(s)} = (s + 1) \times 50, \]

and we convert in the opposite direction like this:

\[ \text{percentage\_to\_similarity(p)} = \frac{p}{50} - 1 \]

Converting in the opposite direction is important because we need to convert the percentages from the traits tab into similarities before feeding them into the cosine similarity formula.

Let's go through an example! Imagine Duolicious only measured extraversion and conscientiousness. Also imagine we have two users, Alex and Taylor. Alex's percentages for extraversion and conscientiousness are 77% and 43%. Taylor's are 60% and 40%. Converted to similarities, we get 0.54 and -0.14 for Alex, and 0.2 and -0.2 for Taylor. Now we plug those into the cosine distance formula from Wikipedia:

\[ \begin{align*} \text{s} \space =& \space \frac{ 0.54 \times 0.2 + (-0.14) \times (-0.2) }{ \sqrt{ (0.54^2 + (-0.14)^2) \times (0.2^2 + (-0.2)^2) } } \\ =& \space \frac{0.136}{\sqrt{0.024896}} \\ \approx& \space 0.86\,. \end{align*} \]

Then:

\[ \text{similarity\_to\_percentage(s)} = 93\%. \]

Phew! Luckily for us, the Duolicious app does this so we don't have to. Now Alex and Taylor can stop busting out their calculators whenever someone asks them on a date.

The Algorithm is Too Complicated. Why Not Compare The Answers Instead of The Traits?

We easily could've calculated the match percentage by asking what percentage of questions two people answered the same way. But there's a few advantages to using traits:

The coolest reason to compare using traits is:

That's because the traits are effectively the interpretation of your answers. They're an understanding of who you are as a person.

If you don't believe us, you could run an experiment for yourself! We're not encouraging you to make two accounts... But we did using a copy of the production database. We had one person make two accounts. Then they answered 100 questions on account A, and a different set of 100 questions on account B. (i.e. they skipped the already-answered questions.) With 350 other users in the database, Duolicious still matched the same person's two accounts with each other. Cool, right?

The Algorithm isn't Complicated Enough

There's plenty of ways to make the algorithm better at the expense of making it more complicated. Even though the current algorithm is pretty good, there's lots of avenues for improvement:

Avenues of improvement aside, we think the Duolicious algorithm is pretty good, and we hope you do too. As Duolicious gets even better, you're gonna see some serious matchmaking going on. We're talking dates so great you'll wonder if it was all a dream. We're talking unparalleled compatibility that feels as if the universe itself conspired to bring the two of you together. So, buckle up, lovebirds! The future of dating is here, and this shit's more magical than you ever imagined!